2020년 10월 모의고사 수학 가형 30번 해설
오늘은 한달 전 시행됐던 10월 모의고사 수학 가형 (이과) 30번 문제 풀이방법에 대하여 알려드리겠습니다.
단순히 한 문제에 대한 풀이로 마치는 것이 아니라 문제를 푸는 근본적인 방법에 대하여 조언해드리니, 킬러문제가 고민이신 분들은 꼭 칼럼을 꼼꼼히 읽어주세요.
먼저 2020년 10월 모의고사 수학 가형 30번 문제를 소개합니다. 아직 문제를 풀어보지 않은 분들은 반드시 풀이를 보기전에 스스로 문제를 풀어보세요.
다음으로, ebsi에 수록되어 있는 공식 풀이방법을 소개해드리겠습니다.
물론 쉬운 문제는 아니였습니다. 그러나 킬러문제중 가장 어렵기로 유명한 30번의 평균 난이도를 고려하면 다른 30번들 보다는 쉬운 편이라 할 수 있습니다.
따라서 30번에 도전하려는 마음가짐으로 이 칼럼에 들어오신 여러분들이라면, 스스로 풀지는 못했더라도 답지 풀이 정도는 충분히 이해하실 수 있을 것입니다.
그러나 항상 가장 중요한 것은 단순 이해를 넘어서, 비슷한 문제가 나오면 내가 스스로 풀 수 있을지, 풀이를 온전히 내 것으로 만들 수 있을지 생각해 보는 것입니다.
지금부터 풀이과정을 하나씩 구체적으로 살펴보며 풀이를 여러분의 것으로 만들 수 있도록 도와드리겠습니다.
첫번째로, f(0) = f(-2)임을 문제에서 제시했습니다. 이차함수이기 때문에 숙련된 분들은 성질을 이용하여 f(x) = kx(x+2) + q 라고 바로 잡을 수 있을 것입니다.
그러나 제가 바람직하다고 평가하는 합리적인 풀이는, 공식 답지처럼 조금 돌아가더라도 "누구나 생각해낼 수 있는 아이디어"입니다.
따라서 바로 식을 잡기가 어렵더라도, f(x)에 0,-2를 대입하여 식을 전개해도 전혀 문제가 없으며 동일한 결론을 유도해 낼 수 있습니다.
첫번째 과정을 통하여 p를 k에 대하여 나타내는 데 성공했습니다. AB < 0 의 형태가 나왔네요. 따라서 두번째로 -1을 기준으로 x 의 범위를 나누는 것은 당연합니다.
아마 대부분의 분들이 아직까지는 의문이 들지 않을 것입니다. 문제는 다음 파트에서 발생합니다.
풀이 자체를 이해하는 분들은 제법 계실 것입니다. 그러나, g'(-1)=-2을 구하는데 갑자기 g', g"을 구하는 이유는 무엇인가요?
그리고 비슷한 문제가 나왔을때 우리는 똑같이 논리를 전개하여 문제를 풀어낼 수 있을까요? 지금부터는 합리적인 논리 전개 방법에 대하여 말씀드리겠습니다.
첫번째로, 우리는 우리가 유도한 이 식을 어떻게 사용할지 고민해봐야 합니다. g(x)가 x = -1의 전후로 mx+m이라는 식과 부호가 바뀌려면 어떻게 해야할까요?
우선 x에 -1을 대입해 g(-1) = -m+m 값이 나와야 합니다. 그래야 부호가 바뀔 수 있는 최소한의 조건이 만족됩니다. 즉 첫번째 식 g(-1) = 0 이 유도됩니다.
그러나 여기서 우리는 하나의 식을 더 생각해내야 합니다. 왜냐하면 g(-1) = 0 은 필요조건일 뿐이지, g(-1) = 0 이라고 해서 주어진 부등호가 반드시 성립하는 것이 아니기 때문입니다.
여기에 식을 만족시키려는 m의 최소값이 2라는 힌트가 주어져 있습니다. 즉 이 식을 이용하여 추가 조건을 구하라는 것을 깨달을 수 있습니다.
저는 이후의 풀이는 공식 풀이와는 조금 다른 방식으로 해결했습니다. 생각해보세요. -1을 기점으로 mx+m와의 대소가 변하려면 어떻게 해야할까요?
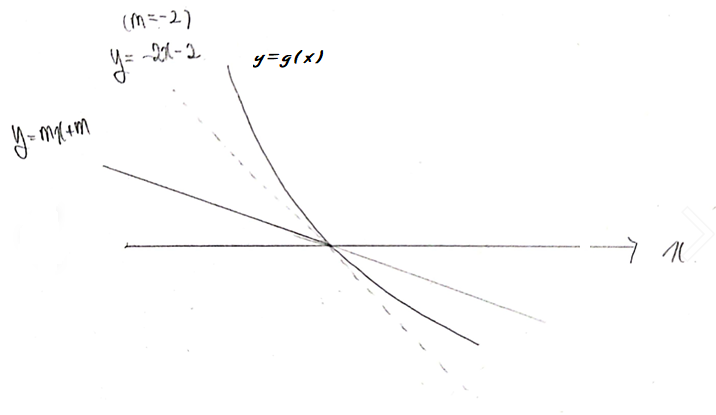
반드시 그림과 같은 형태가 나와야합니다. 즉 함수값이 같은 것 뿐만 아니라 반드시 m이 g'(-1)보다는 크거나 같아야 한다는 것이죠. 이때 m의 최소값이 -2이므로, g'(-1) = -2 가 되는 것은 자명합니다.
이제 두 식을 연립하여 다음 식을 유도할 수 있습니다.

이 식은 문자 3개, 식1개의 형태입니다. 즉 2개의 식만 더 있으면 문제를 풀어낼 수 있습니다. 이제 (나)식을 한번 살펴볼까요?
(나) 조건은 딱 두개의 식을 구할 수 있도록 되어 있습니다. 또한 g(x)는 지수 위의 식을 미분하면 아래의 함수가 나오는 형태기 때문에, 매우 적분하기 쉽습니다.
따라서 이제 문자 3개, 식3개, a,k,q를 모두 구할 수 있다는 것입니다. 문제의 풀이를 단순히 쭉 읽어봤을때는 스스로 풀기가 어렵다고 생각할 수 있습니다.
그러나 하나씩 과정을 살펴보며 왜 이런 아이디어를 사용 할까?에 초점을 맞추어 복습을 한다면, 문제를 푸는 것이 점점 쉬워진다는 것을 느낄 수 있습니다.
여러분들 스스로도 "내가 왜 이러한 방식으로 논리를 전개해나가고 있을까" 라는 질문을 스스로 던지며 문제를 풀어보세요. 근본적인 실력이 크게 향상될 것입니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
개인적으로 연계 공부에 굉장히 부정적인 입장이라 올해 수능을 보기까지 개인적으로는...
-
오타랑 비문, 문제 자체검수도 하다보니 7시간이나 걸림;; 초안은 4시간컷인데 졸려죽겟네
-
지구 1컷 0
44라는 여론들이 왜 점점 많아지는거 같죠 ㅋㅋㅋ 다수 업체들 예상처럼 1컷 42이길...!
-
등급컷 0
님들 물리 1컷 46될 가능성은 없나여? 지구 2컷 38될 가능성도...
-
롤 정신병 걸릴것같아.... 탑레 다이아, 현재 에메-플레 지옥에 빠짐 오버워치...
-
언매 vs 화작 0
재수 준비하고 있는데 언매 할지 화작 할지 고민중입니다 이번 수능에서 화작 15분...
-
치타는 울다가 웃어서 엉덩이에 털났다.
-
반갑습니다. 18
-
사실상 오지 말라죠? 최고점-최저점 20점 이상이냐 이하냐에 따라 다르지만
-
지금 6등급이구. . . 일단새벽 6시-7시 20분까지 모의고사연습 9시까지...
-
3월 말부터 공부하면요 ㅠ
-
정상화좀
-
일단 3월부터 수능날까지 매일 3-4시간 투자할거고 3월말부터개념,기출 들이박고...
-
33257수의대 1
과탐은 올해하다가 놧는데 재수하면 수의대 갈 수 잇을까요 과탐은 생지로 바꾸려합니다
-
님들 나 어때? 1
나 진심 문제 있는걸까. . 너무 불안해
-
생지랑 정도 많이들었고, 쏟은 시간이 아까워서 사탐런을 하기 망설여집니다 우선...
-
ㄹㅇ 중간에 정병왔을거같음 국어 5월중순인가에 풀려서 경기도에서 버스타고 갔는데...
-
가채점 지금 진학사나 메가에서 점수 주는 거 확통틀이면 표점 우세한 거 반영되어있나요?
-
생각보다 꽤 많은 동아리가 나이 많으면 컷합니다 지금 기준 9n부터는 신입컷하더라구요
-
학교 다니면서 느낌 진짜 있음 그냥 나랑 다른거라 부럽다거나 그런 느낌도 안듦걍...
-
고1이고 스카다니고있는데 중학생들 시험기간되면 너무 시끄럽고 사람이 많아서 집가까운...
-
고인물임
-
언매 91 미적 공통-2 미적-1 틀림 88 영어 4등급 생명 45 지구42...
-
31411 정시 문과라인 어디까지일까요? 정시는 처음입니다 2
국어 78 언매 수학 88 미적 영어4 정법 47 사문47 입니다 문과라인 어디까지...
-
연세대 이 트래쉬 잡대 대체 가스라이팅을 어캐했길래 애들이 계속 연대한다 연대한다...
-
오랜만에 메가나 들어가볼까 해서 갔는데 2타시네요..? ㄷㄷ 양승진t가 4타 되시고..
-
고교 출결때문에 암만 높여봐도 97점이네... 5월 입대 노리고있는데 이거...
-
학고반수 실패에 관해 질문 답변.. 제발 부탁드립니다.. 2
1학년 1학기 아예 학교 안다니고, 2학기는 휴학했습니다. 학사경고장은 받았습니다....
-
탐구 고민 0
과탐 1 2 각각 뭐 해야하죠? 물1 지2?
-
올해같은 입시에서 서울대 의치대는 cc면 힘든가요? 0
어떻지 모름
-
감점폭도 크고 비교내신도 안 주는 이유는 메디컬 때문같음 그리고 수시 출신이나 내신...
-
예체능이라 수학 빼고 저 성적 나왔습니다 .. 재수때 나름 거의 아침부터 열심히...
-
으아아아ㅏ아ㅏ 잘래
-
생1은 개념형 다풀고 근수축 막전위 푼후 4문제 찍어서 하나 맞추면 개날먹으로...
-
어지간하면 bb아님 cc 둘 중에서 준다던데 cc는 얼마나 까이는 거임...
-
반드시 ㄱㄱ헛
-
이거 채용조건형임??? sk나 삼전??
-
그냥 얼굴 때문이 아니라 돈버는게 얼마나 ㅈ같고 고된건지 알면 알수록 짜증이남
-
논술 질문 0
제가 a에서 선분 cd에 내린 수선과 cd가 만나는점을 h라하자를 a에서 선분...
-
형 잔다. 2
오르비 취침소등하겠습니다. 편안한 밤 되십시오!
-
하.......예전에는 하루에 2쿨도 봤는데
-
cc라면?
-
본인들은 의대 가서 전문의 따는게 가성비가 어떻다 생각함? 그니까 의대 가기 위한...
-
평소에 잘 하다가 재수 수능 딱 한 번 망치니까 진짜 살기 싫음
-
낮과 추추합은 노려볼만하겠죠?
-
보다보다 어지러워서 잘거임뇨..
-
하. . . 사탐런할거면 얘로 가야할까요?
-
재수 시작하기 전까지 알바 투잡 존나 하셈 그리고 햇살론대출로 몇백 대출 땡기고...
-
1학년때부터 지금까지 제대로 국어 공부라는걸 해 본적이 없음.. 독서 기출만...






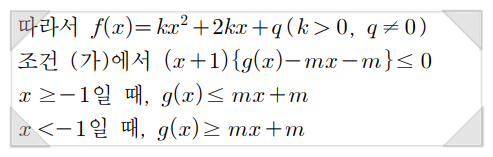

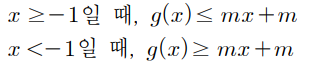






























이따가 공부 끝내고 읽어볼게요